数値解析・計算科学，およびそれを含む応用数学・数理工学
現代科学・工学の最先端で挑戦する諸問題は、もはや解析的に解くことは難しく、計算機の助けを借りねばなりません。どうやって解くべきか、それで解いたときの数学的保証は何か、を総合的に研究する学問が数値解析です。応用（物理、生物、経済など）、数学（解析、代数、幾何など）、および計算機の知識 （プログラミング、並列化など）の３つの分野を横断し、様々な始点から研究テーマを設定できる奥の深い学問です。数値解析はオイラー、ガウスの時代からの系譜を持つ歴史の長い学問であり、それだけに莫大な研究の蓄積がありますが、他方で前述のように非常に対象・手法の範囲が広い学問分野であるため、「隙間」のように見落とされてきた（しかしながら重要な）話題も多く、着眼とアイデア次第で、いきなり優れた結果が出せることも多々あるのも魅力です。
数値解析的な話題をを主軸としつつ、より特定の応用そのものに興味を抱く場合には、学問分野として「計算科学」と呼ぶこともあります。計算科学は科学のスタイルの一種で、実験科学（第一の科学）、理論科学（第二の科学）に続く、第三の科学であると言われています。直ちに（現実の）実験もできないし、紙と鉛筆で理論的に探究することもむつかしいが、計算機の中に実験室を作って調べることはできる、そのような分野を探求する学問スタイルを言います。いわゆる物理シミュレーションに代表される、シミュレーションに基づく研究分野です。我々の研究室では、そのような研究も対象としています。
なお、いま現在は、第三の科学を超えて、第四の科学、すなわち「データ駆動型科学」（莫大に得られる実データと統計手法・機械学習的手法を積極的に組み合わせて行う新しい科学研究スタイル）の時代だと言われています。そのような時代においても、「計算機の助けを借りて数値的に処理をして問題に挑戦する」構造に変わりはなく、依然として数値解析学的な考え方は基本的なツールとなります。この意味で「第四の科学時代の基礎を支える」手法を数値解析学的視点から確立すること、および反対に、従来の数値解析学に第四の科学の知見を入れてバージョンアップを目指していくことも、本研究室の重要な研究テーマのひとつです。
以下では、これまで研究室各教員が研究してきた具体的なトピックをいくつか例示します。
構造保存型数値解法
計算機で解こうとする問題を、その物理的背景、あるいはそれに対応する抽象的数理構造まで踏み込んで捉え、通常の算法を遥かに上回る数値計算法を生み出すことを「構造保存型」の数値計算法と呼びます。
物理や化学、生物学、あるいは経済学などの問題はしばしば微分方程式で数理モデル化され、それを様々な手法で離散化（有限次元化）して計算機に載せて解く、それが数値計算という技法です。これはオイラーやガウスの時代から数百年にわたって（計算機発明より遥か前から！）行われてきましたが、長らく、その研究の手法は「数理モデルをどう離散化するか」に留まっていました。それが1990年代ころから、「おおもとの物理（化学、…）の問題に立ち返って、どう計算すべきかを考える」手法がより優れた計算結果を導くことが明らかになりました。このような手法では、しばしば数理モデルに内在する抽象的数理構造（しばしば幾何学的構造）を尊重し保存するため、「構造保存型数値解法」と呼ばれ、いまでは現代数値解析学の主要な研究分野のひとつとなっています。本研究室は、日本初の強力な手法を提案・発展してきた実績があり、この分野で世界的拠点のひとつです。
この分野の研究については、松尾のＨＰも併せてご覧ください。
高精度な関数近似法などの設計・解析・応用
関数近似法は数値微分や数値積分、関数方程式の近似解法など、多くの解析系数値計算法の源流となる手法です。幅広い応用を持つだけでなく、数学的に興味深い理論も多くあります。
関数は一般に無限次元空間に属し、それを計算機で扱うためにどう有限次元近似するかは自明ではありません。被近似関数のクラスごとに適した近似法が研究されており、科学・工学が進化して新しい問題が出てくるごとに、常に新しい関数近似が考えられています。また、それらを基にして数値積分法や関数方程式の近似解法が設計されています。
これまで主に扱ってきた方法として、sinc関数（sin(x)/x）による方法（Sinc法）があります。これは解析関数の近似にとても向いていることが知られています。特に、日本発の強力な手法である「二重指数関数型変換」（高橋・森）と相性が良く、それと組み合わせたSinc法（DE-Sinc法）は、微分方程式や積分方程式など、様々な問題に対して強力なツールとなることが分かっています。また、関連の深い方法として、DE-Sinc法に先立って考案された数値積分法である「二重指数関数型公式」（高橋・森）があり、高精度で有用な公式として良く知られています。これらの方法はいずれも、適切な関数空間の設定のもとで準最適な精度を達成することも理論的に示されています。
さらに近年では、同様の関数空間における最適性の基準をもとにして、数理最適化による一定の方法で、より高精度な公式を設計する方法にも取り組んでいます。今後は、これらの方法をより一般的な設定へと展開していくことが課題となっています。
この分野の研究については、田中のＨＰも併せてご覧ください。
多重格子法（Multigrid法）
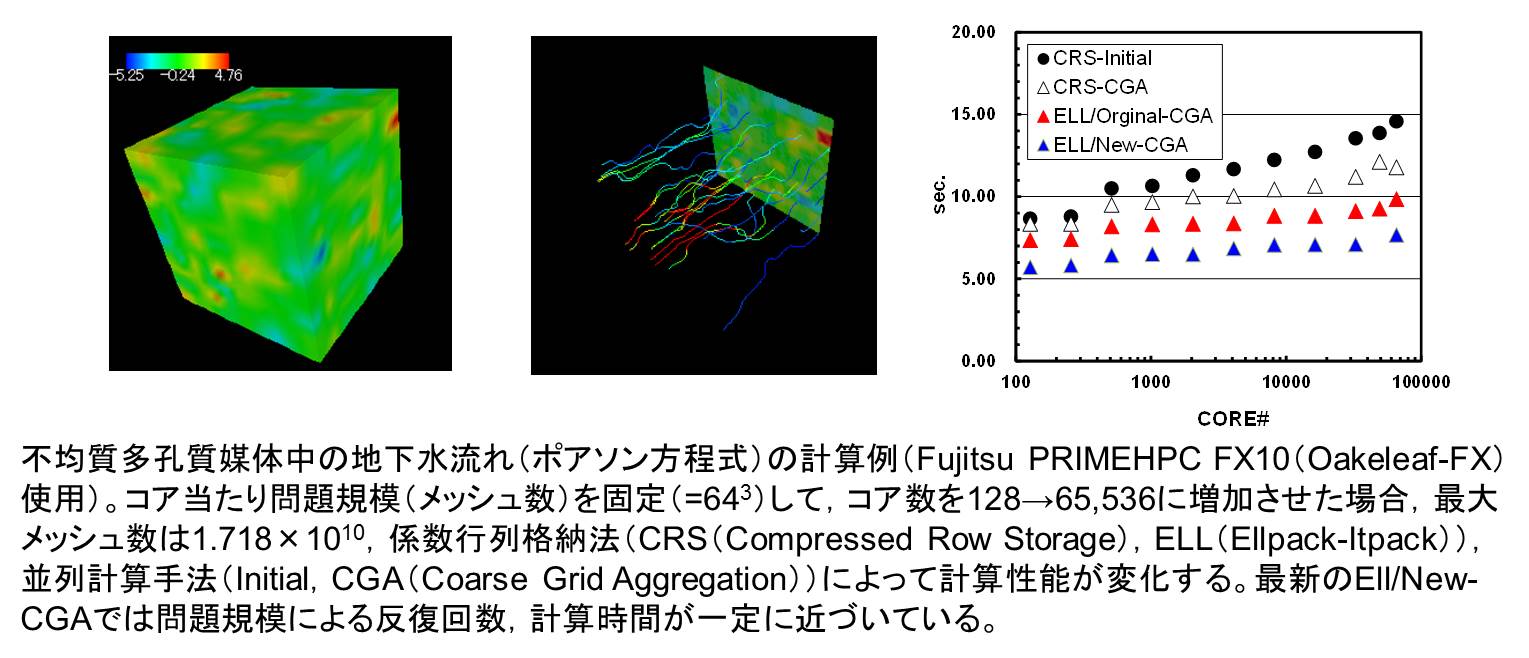
有限要素法、差分法などによる数値シミュレーションは最終的には、
疎行列を係数行列とする大規模な連立一次方程式を解くことに帰着されます。
連立一次方程式解法としては共役勾配法（Conjugate Gradient、CG）に代表される反復法がよく使われています。
多重格子法（Multigrid、MG）は、様々な波長の誤差成分を同時に減衰させる性質があり、高速に収束するとともに、反復回数が問題規模に依存しません。
特にMGをCG法の前処理手法とするMGCG法は大規模問題向けの並列解法として有効です。
様々な複雑な問題向けのアルゴリズムの研究開発を実施しています。
この分野の研究については、中島のＨＰも併せてご覧ください。